1. Uitleg talstelsels

Wat is een talstelsel?

Een talstelsel is een wiskundig systeem om getallen te representeren. Je gebruikt het dagelijks als je getallen opschrijft.

Hoe zit een talstelsel in elkaar?

Wij maken gebruik van positiestelsels. Hiermee bedoelen we dat de posities van de symbolen uitmaakt:

$$\begin{gathered} 123\ne 321 \\ 0011\ne 1100 \end{gathered}$$

Dit zijn een aantal voorbeelden van talstelsels:

Talstelsel	Voorbeeld
Romeinse cijfers	CXXIII
Decimaal	123
Binair	1111011
Hexadecimaal	7B
Octaal	755

Het decimale talstelsel

Wij maken in het dagelijks leven gebruik van het decimale talstelsel (of tientallig talstelsel). Dit stelsel heeft als grondtal 10 en als symbolen de getallen 0 .. 9.

In het decimale talstelsel kunnen we elk getal schrijven als een optelsom van machten van grondtal 10. Bijvoorbeeld:

$$\begin{array}{ccccccc}725& =& 700& +& 20& +& 5\\ & =& 7\cdot 100& +& 2\cdot 10& +& 5\cdot 1\end{array}$$

Aangezien $10^0=1$, $10^1=10$, $10^2=100$, $10^3=1000$, etc., kunnen we het getal 725 in het decimale talstelsel schrijven als een optelsom van machten van het grondtal $10$:

$$\begin{array}{ccccccc}725& =& 7\cdot {10}^2& +& 2\cdot {10}^1& +& 5\cdot {10}^0\end{array}$$

Het binaire talstelsel

Hetzelfde principe geldt voor andere talstelsels. Neem bijvoorbeeld het binaire talstelsel. Dit stelsel heeft als grondtal 2 en als symbolen de getallen 0 en 1.

In het binaire stelsel kunnen we elk getal schrijven als een optelsom van machten van grondtal $2$. Bijvoorbeeld:

$$\begin{array}{ccccccc}101_2& =& 1\cdot 2^2& +& 0\cdot 2^1& +& 1\cdot 2^0\\ & =& 1\cdot 4& +& 0\cdot 2& +& 1\cdot 1\\ & =& 4& +& 0& +& 1\\ & =& 5& & & & \end{array}$$

Notatie

Onder “101” staat een 2. Dit geeft aan dat 2 het grondtal van 101 is. Als het grondtal 10 is, dan wordt deze vaak weggelaten. Uit bovenstaande uitwerking kunnen kunnen we concluderen dat $1011_2=5_{10}$.

Hexadecimale talstelsel

Het hexadecimale talstelsel is een andere naam voor het zestientallige talstelsel. Dit talstelsel heeft als grondtal 16. Je zou de symbolen 0 t/m 15 verwachten, maar de getallen boven 9 nemen meer dan 1 positie in beslag. Daarom is gekozen om na 9 door te nummeren met A, B .. F (A=10, B=11, C=12, .. , F=15).

In het hexadecimale stelsel kunnen we elk getal schrijven als een optelsom van machten van grondtal $16$. Bijvoorbeeld:

$$\begin{array}{c}\begin{array}{ccccccc}24{\text{E}}_2& =& 2\cdot {16}^2& +& 4\cdot {16}^1& +& 14\cdot {16}^0\\ & =& 2\cdot 256& +& 4\cdot 16& +& 14\cdot 1\\ & =& 512& +& 64& +& 14\\ & =& 590& & & & \end{array}\end{array}$$

Terminologie

De getallen die vermenigvuldigd worden met de machten noemen we vermenigvuldigingsfactoren of kortweg factoren.

Gegeven deze vergelijking:

$2\cdot 16^2+4\cdot 16^1+14\cdot 16^0$

Hierin zijn 2, 4 en 14 de factoren.

Talstelsels in de informatica

In de informatica maken we veel gebruik van de volgende 3 talstelsels:

Talstelsel	Grondtal	Symbolen
Binair	2	0, 1
Octaal	8	0-7
Hexadecimaal	16	0-9, A-F

Een binair getal van $n$ bits kan $2^n$ getallen representeren. Omdat een binair getal van $n$ bits precies $2^n$ getallen kan representeren, komt 1 cijfer uit bovenstaande talstelsels altijd precies overeen met 1 / 3 / 4 bits.

Hoe gebruik je talstelsels?

• Octaal
  • Linux: chmod
• Hexadecimaal
  • Kleurcodes
  • Spaties in URLs: www.example.com/name%20with%20spaces
    • Kopieer deze string eens als URL: %77%77%77%2E%6E%75%2E%6E%6C
  • Geheugenadressen
• Binair
  • Compressie van data

Talstelsels en computers

Term	Uitleg
Word	De eenheid van data in een processor noemen we een Word
Woordlengte	Een word heeft een vaste woordlengte. Tegenwoordig bestaan woordlengtes van 64, 32 of 16 bits
Byte	Een byte is een woord van 8 bits. Een byte kan je ook beschouwen als een karakter, een letter of een teken

Byte

Aangezien een byte bestaat uit 8 bits, kunnen we er $2^8=256$ getallen mee representeren. We kunnen een byte ook representeren door 2 hexadecimale cijfers (immers $16\cdot 16=256$).

Een byte kan je beschouwen als een karakter, een letter, een teken. Zie hiervoor de ASCII tabel:

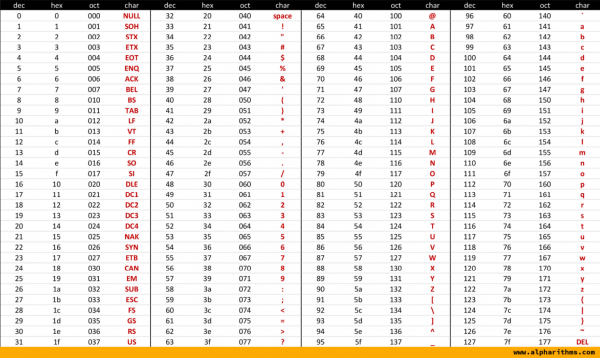Figuur 1: ASCII tabel

Bronnen

Talstelsels: https://nl.wikipedia.org/wiki/Talstelsel
Positiestelsel: https://nl.wikipedia.org/wiki/Positiestelsel
Binair talstelsel: https://nl.wikipedia.org/wiki/Binair_talstelsel
Octaal talstelsel: https://nl.wikipedia.org/wiki/Octaal_talstelsel
Hexadecimaal talstelsel: https://nl.wikipedia.org/wiki/Hexadecimaal_talstelsel

---

Volgende stap: Stappen omzetten naar decimaal